悢妛偺儁乕僕
Question侾
Q1 弌戣擔:2009.6/14(擔)丂昁梫側抦幆: 崅峑悢妛B儗儀儖
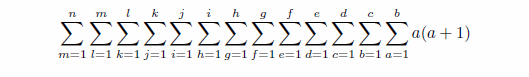
傪媮傔傛丅
夝摎偲夝愢
乮摎偊偺悇應乯
偳偆峫偊偰傕嚁偑懡偡偓傑偡傛偹丅偠傖偁丄偳偆傗偭偰庤傪偮偗偰峴偒傑偟傚偆偐丅
偙偺庤偺栤戣偼傑偢丄乽偨偔偝傫偁傞傕偺傪尭傜偡乿偙偲偑桳岠偱偡丅 偙偺栤戣偱偨偔偝傫偁傞傕偺偼儼偱偡丅偱偼嚁傪1屄偵偟傒偨傜偳偆偱偟傚偆丅
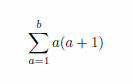
偙傟側傜娙扨偩偲巚偄傑偡丅
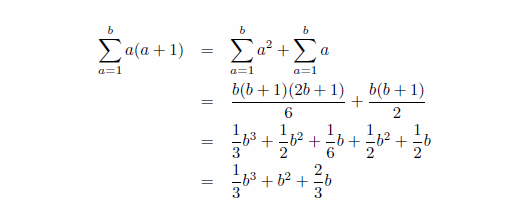
傑偁丄悢妛B偺婎杮揑側栤戣偱偟偨偹丅
偱偼丄堦懅偮偄偨偲偙傠偱乽偨偔偝傫偁傞傕偺傪尭傜偡乿
偙偲偺堄枴傪彮偟夝愢偟傑偡丅娙扨偵偄偊偽丄偨偔偝傫偁傞傕偺傪尭傜偟偨栤戣偲偄偆偺偼尦偺栤戣偺僸儞僩偵側傞傢偗偱偡丅
椺偊偽丄師偺傛偆側応崌偱偡丅
丂悢傪尭傜偟偨栤戣偐傜壗傜偐偺朄懃傪梊應偱偒傞応崌丅
丂悢偑懡偄栤戣偲夝朄偑摨偠偱偁傞応崌丅
丂悢傪尭傜偟偨栤戣偺摎偊偑悢偑懡偄栤戣傪夝偔偺偵捈愙棙梡偱偒傞応崌丅
偙偺偙偲偼偄偔偮傕偺栤戣傪偙側偟偰姶偠偰偄偗偽偄偄偲巚偄傑偡丅
偦傟偱偼栤戣偵栠傝傑偡偑丄偝偭偒偺栤戣偵偪傚偭偲晅偗懌偟偑偁傝傑偡丅悢傪尭傜偟偨栤戣傪夝偄偨偺偼尦偺栤戣偺僸儞僩傪摼傞偨傔偱偟偨偹丅偮傑傝丄偙偺栤戣偺摎偊偼揥奐偟偨宍偲場悢暘夝偟偨宍偺椉曽偱昞傢偟偲偄偨傎偆偑偄偄傢偗偱偡丅
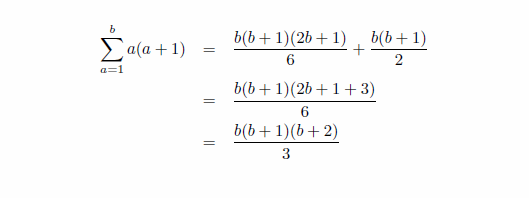
偪傚偭偲偍傕偟傠偄幃偑弌偰偒傑偟偨丅暘曣偵拲栚偡傞偲a(a+1)偐傜b(b+1)(b+2)偵曄壔偟偰偄傑偡丅側傫偐朄懃惈偑偁傝偦偆偱偡丅偱偼丄暘巕偺3偼壗偱偟傚偆丅傑偩庤偑偐傝偑懌傝傑偣傫偹丅傕偆偡偙偟僸儞僩廤傔傪懕偗傑偡丅
師偼嚁傪2屄偵偟偰峫偊偰傒傑偡丅
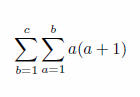
偙偺栤戣傪夝偔慜偵傂偲偮妋擣丅

忋偺岞幃丄抦偭偰傑偡偐丅栤戣廤偵偼悢俛偺婎杮帠崁偲偟偰晛捠偵嵹偭偰傞傫偱偡偗偳丄巹偺庤帩偪偺嫵壢彂偵偼抧枴偵偟偐嵹偭偰側偄傫偱偡傛偹乕丅抦傜側偄偲偙偺栤戣偼偮傜偄偱偡丅偛傔傫側偝偄丅
偲偄偆偙偲偱丄偙偙偱傕悢俛偺婎杮帠崁偲偟偰晛捠偵巊傢偣偰偄偨偩偒傑偡丅

偩偄傇朄懃惈偑尒偊偰偒偨偱偟傚偆偐丅偙偙傑偱偺擇偮偺幃傪傑偲傔偰傒傑偡丅


暘曣偼a(a+1)仺b(b+1)(b+2)仺c(c+1)(c+2)(c+3)偱偡偐傜師偼d(d+1)(d+2)(d+3)(d+4)偩偲娙扨偵梊應偱偒傑偡丅
暘巕偼1仺1/3仺1/3丒1/4丂偲偒偰偄傑偡丅偍偦傜偔師偼丄1/3丒1/4丒1/5偱偟傚偆丅
偱偼丄尦偺栤戣傪梊應偟傑偡丅嚁偺悢偑13屄偁傝傑偟偨偐傜丄